Системой линейных уравнений называется совокупность рассматриваемых совместно нескольких линейных уравнений.

В системе может быть любое число уравнений с любым числом неизвестных.

Решением системы уравнений называется совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, то есть обращающая их в тождества.

Система, имеющая решение, называется совместной, в противном случае – несовместной.

Для решения системы применяют различные методы.

Пусть
(число уравнений равно числу неизвестных).

Метод Крамера

Рассмотрим решение системы трёх линейных уравнений с тремя неизвестными:

(7)

Для нахождения неизвестных
применим формулу Крамера:

(8)

где - определитель системы, элементы которого есть коэффициенты при неизвестных:

.

получается путём замены первого столбца определителя столбцом свободных членов:

.

Аналогично:

;
.

Пример 1. Решить систему по формуле Крамера:

.

Решение: Воспользуемся формулами (8):

;

;

;

;

Ответ:
.

Для любой системы линейных уравнений снеизвестными можно утверждать:

Матричный способ решения

Рассмотрим решение системы (7) трёх линейных уравнений с тремя неизвестными матричным способом.

Используя правила умножения матриц, данную систему уравнений можно записать в виде:
, где

.

Пусть матрица невырожденная, т.е.
. Умножая обе части матричного уравнения слева на матрицу
, обратную матрице, получим:
.

Учитывая, что
, имеем

(9)

Пример 2. Решить систему матричным способом:

.

Решение: Введём матрицы:

- из коэффициентов при неизвестных;

- столбец свободных членов.

Тогда систему можно записать матричным уравнением:
.

Воспользуемся формулой (9). Найдём обратную матрицу
по формуле (6):

;

.

Следовательно,

Получили:

.

Ответ:
.

Метод последовательного исключения неизвестных (метод Гаусса)

Основная идея применяемого метода заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе трёх уравнений с тремя неизвестными:

.

Допустим, что
(если
, то изменим порядок уравнений, выбрав первым уравнением то, в котором коэффициент прине равен нулю).

Первый шаг: а) делим уравнение
на
; б) умножаем полученное уравнение на
и вычитаем из
; в) затем полученное умножаем на
и вычитаем из
. В результате первого шага будем иметь систему:

,

Второй шаг: поступаем с уравнением
и
точно так же, как с уравнениями
.

В итоге исходная система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно без труда.

Замечание. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов, при неизвестных, и свободных членов.

Пример 3. Решить методом Гаусса систему:

.

Переход от одной матрицы к другой будем записывать при помощи знака эквивалентности ~.

~
~
~
~

~
.

По полученной матрице выписываем преобразованную систему:

.

Ответ:
.

Замечание: Если система имеет единственное решение, то ступенчатая система приводится к треугольной, то есть к такой, в которой последнее уравнение будет содержать одно неизвестное. В случае неопределённой системы, то есть такой, в которой число неизвестных больше числа линейно независимых уравнений, треугольной системы не будет, так как последнее уравнение будет содержать более одного неизвестного (система имеет бесчисленное множество решений). Когда же система несовместна, то, после приведения её к ступенчатому виду, она будет содержать хотя бы одно значение вида
, то есть уравнение, в котором все неизвестные имеют нулевые коэффициенты, а правая часть отлична от нуля (система решений не имеет). Метод Гаусса применим к произвольной системе линейных уравнений (при любых
и).

Теорема существования решения системы линейных уравнений

При решении системы линейных уравнений методом гаусса ответ на вопрос, совместна или несовместна данная система может быть дан лишь в конце вычислений. Однако часто бывает важно решить вопрос о совместности или несовместности системы уравнений, не находя самих решений. Ответ на этот вопрос даёт следующая теорема Кронекера-Капелли.

Пусть дана система
линейных уравнений снеизвестными:

(10)

Для того, чтобы система (10) была совместной, необходимо и достаточно чтобы ранг матрицы системы

.

был равен рангу её расширенной матрицы

.

Причём, если
, то система (10) имеет единственное решение; если же
, то система имеет бесчисленное множество решений.

Рассмотрим однородную систему (все свободные члены равны нулю) линейных уравнений:

.

Эта система всегда совместна, так как она имеет нулевое решение .

В следующей теореме даны условия, при которых система имеет также решения, отличные от нулевого.

Терема. Для того, чтобы однородная система линейчатых уравнений имела нулевое решение, необходимо и достаточно, чтобы её определитель был равен нулю:

.

Таким образом, если
, то решение- единственное. Если
, то существует бесконечноё множество других ненулевых решений. Укажем один из способов отыскания решений для однородной системы трёх линейных уравнений с тремя неизвестными в случае
.

Можно доказать, что если
, а первое и второе уравнения непропорциональны (линейно независимы), то третье уравнение есть следствие первых двух. Решение однородной системы трёх уравнений с тремя неизвестными сводится к решению двух уравнений с тремя неизвестными. Появляется так называемое свободное неизвестное, которому можно придавать произвольные значения.

Пример 4. Найти все решения системы:

.

Решение. Определитель этой системы

.

Поэтому система имеет нулевые решения. Можно заметить, что первые два уравнения, например, непропорциональны, следовательно, они линейно независимые. Третье является следствием первых двух (получается, если к первому уравнению прибавить удвоенное второе). Отбросив его, получим систему двух уравнений с тремя неизвестными:

.

Полагая, например,
, получим

.

Решая систему двух линейных уравнений, выразим ичерез:
. Следовательно, решение системы можно записать в виде:
, где- произвольное число.

Пример 5. Найти все решения системы:

.

Решение. Нетрудно видеть, что в данной системе только одно независимое уравнение (два других ему пропорциональны). Система из трёх уравнений с тремя неизвестными свелась к одному уравнению с тремя неизвестными. Появляются два свободных неизвестных. Найдя, например, из первого уравнения
при произвольныхи, получим решения данной системы. Общих вид решения можно записать, гдеи- произвольные числа.

Вопросы для самопроверки

Сформулируйте правило Крамера для решения системы линейных уравнений снеизвестными.

В чём сущность матричного способа решения систем?

В чём заключается метод Гаусса решения системы линейных уравнений?

Сформулируйте теорему Кронекера-Капелли.

Сформулируйте необходимое и достаточноё условие существования ненулевых решений однородной системы линейных уравнений.

Примеры для самостоятельного решения

Найдите все решения систем:

1.
; 2.
;

3.
; 4.
;

5.
; 6.
;

7.
; 8.
;

9.
; 10.
;

11.
; 12.
;

13.
; 14.
;

15.
.

Определите, при каких значениях исистема уравнений

а) имеет единственное решение;

б) не имеет решения;

в) имеет бесконечно много решений.

16.
; 17.
;

Найти все решения следующих однородных систем:

18.
; 19.
;

20.
; 21.
;

22.
; 23.
;

Ответы к примерам

1.
; 2.
; 3. Ǿ; 4. Ǿ;

5.
- произвольное число.

6.
, где- произвольное число.

7.
; 8.
; 9. Ǿ; 10. Ǿ;

11.
, где- произвольное число.

12. , гдеи- произвольные числа.

13.
; 14.
гдеи- произвольные числа.

15. Ǿ; 16. а)
; б)
; в)
.

17. а)
; б)
; в)
;

18.
; 19.
; 20., где- произвольное число.

21. , где- произвольное число.

22. , где- произвольное число.

23. , гдеи- произвольные числа.

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
-

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы - (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

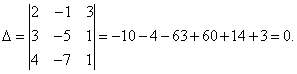
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко ходить не надо.

Следующий пример - на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

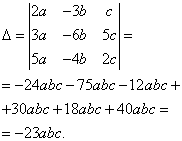
Находим определители при неизвестных

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел - матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин "матрица" появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A mn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов .

Элементы матрицы a ij , у которых i=j, называются диагональными и образуют главную диагональ .

Для квадратной матрицы (m=n) главную диагональ образуют элементы a 11 , a 22 ,..., a nn .

Равенство матриц.

A=B , если порядки матриц A и B одинаковы и a ij =b ij (i=1,2,...,m; j=1,2,...,n)

Действия над матрицами.

1. Сложение матриц - поэлементная операция

Вычитание матриц - поэлементная операция

3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A mk *B kn =C mn причем каждый элемент с ij матрицы C mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B.

Покажем операцию умножения матриц на примере:

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A T или A"

Строки и столбцы поменялись местами

Пример

Свойства опeраций над матрицами

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

Виды матриц

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1 . Например, (1 3 5 7) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1 . Например

5. Диагональная матрица: m=n и a ij =0 , если i≠j . Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a ij =0, i=1,2,...,m

j=1,2,...,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

9. Квадратная матрица:m=n и a ij =a ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательноA"=A

Например,

Обра́тная ма́трица - такая матрица A −1 , при умножении на которую исходная матрица A даёт в результате единичную матрицу E :

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Примеры решения систем линейных алгебраических уравнений матричным методом.

Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц.

Пример.

С помощью обратной матрицы найдите решение системы линейных уравнений

.

Решение.

В матричной форме исходная система запишется как, где . Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем , следовательно, для матрицы А может быть найдена обратная матрица . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как . Итак, задача свелась к построению обратной матрицы . Найдем ее.

Обратную матрицу можно найти по следующей формуле :

, где – определитель матрицы А, – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Понятие обратной матрицы существует только для квадратных матриц , матриц «два на два», «три на три» и т.д.

Полярные координаты. В полярной системе координат положение точки М

М

ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ В ПРОСТРАНСТВЕ

ПРЯМАЯ

1. Общее уравнение прямой. Всякое уравнение первой степени относительно х и у, т. е. уравнение вида:

(1) Ах+Ву+С=0 наз. общин уравнением прямой ( + ≠0),A,B,C-ПОСТОЯННЫЕ КОЭФИЦИЕНТЫ.

КРИВЫЕ ВТОРОГО ПОРЯДКА

1. Окружность. Окружность-это множество точек плоскости, равноудален-

равноудаленных от данной точки (центра). Если г - радиус окружности, а точка С (а; Ь) - ее центр, то уравнение окружности имеет вид:

Гипербола . Гиперболой называется множество точек плоскости, абсолютная

величина разности расстояний которых до двух данных точек, называемых фо-

кусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Если поместить фокусы гиперболы в точках F1 (с; 0) и F2(- с; 0), то получится каноническое уравнение гиперболы

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

ПЛОСКОСТЬ И ПРЯМАЯ

плоскости,называемый нормальным вектором.

Поверхность второго порядка

Поверхность второго порядка - геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов , , , , , отличен от нуля.

Типы поверхностей второго порядка

Цилиндрические поверхности

Поверхность называется цилиндрической поверхностью с образующей , если для любой точки этой поверхности прямая, проходящая через эту точку параллельно образующей , целиком принадлежит поверхности .

Теорема (об уравнении цилиндрической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность имеет уравнение , то - цилиндрическая поверхность с образующей, параллельной оси .

Кривая, задаваемая уравнением в плоскости , называется направляющей цилиндрической поверхности.

Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка .

Эллиптический цилиндр:	Параболический цилиндр:	Гиперболический цилиндр:
Пара совпавших прямых:	Пара совпавших плоскостей:	Пара пересекающихся плоскостей:

Конические поверхности

Коническая поверхность.

Основная статья: Коническая поверхность

Поверхность называется конической поверхностью с вершиной в точке , если для любой точки этой поверхности прямая, проходящая через и , целиком принадлежит этой поверхности.

Функция называется однородной порядка , если выполняется следующее:

Теорема (об уравнении конической поверхности).
Если в некоторой декартовой прямоугольной системе координат поверхность задана уравнением , где - однородная функция, то - коническая поверхность с вершиной в начале координат.

Если поверхность задана функцией , являющейся однородным алгебраическим многочленом второго порядка, то называется конической поверхностью второго порядка .

· Каноническое уравнение конуса второго порядка имеет вид:

Поверхности вращения ]

Поверхность называется поверхностью вращения вокруг оси , если для любой точки этой поверхности окружность, проходящая через эту точку в плоскости с центром в и радиусом , целиком принадлежит этой поверхности.

Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность задана уравнением , то - поверхность вращения вокруг оси .

Эллипсоид:	Однополостной гиперболоид:	Двуполостной гиперболоид:	Эллиптический параболоид:

В случае, если , перечисленные выше поверхности являются поверхностями вращения.

Эллиптический параболоид

Уравнение эллиптического параболоида имеет вид

Если , то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы, параметр которой , вокруг вертикальной оси, проходящей через вершину и фокус данной параболы.

Пересечение эллиптического параболоида с плоскостью является эллипсом.

Пересечение эллиптического параболоида с плоскостью или является параболой.

Гиперболический параболоид ]

Гиперболический параболоид.

Уравнение гиперболического параболоида имеет вид

Пересечение гиперболического параболоида с плоскостью является гиперболой.

Пересечение гиперболического параболоида с плоскостью или является параболой.

Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

Центральные поверхности

Если центр поверхности второго порядка существует и единственен, то его координаты можно найти, решив систему уравнений:

Таким образом, знак, который при этом приписывается минору соответствующего элемента определителя, пределяется следующей таблицей:

В приведенном выше равенстве, выражающем определитель третьего порядка,

в правой части стоит сумма произведений элементов 1-й строки определителя на их алгебраические дополнения.

Теорема 1. Определитель третьего порядка равен сумме произведений

элементов любой его строки или столбца на их алгебраические дополнения.

Эта теорема позволяет вычислять значение определителя, раскрывая его по

элементам любой его строки или столбца.

Теорема 2. Сумма произведений элементов какой-либо строки (столбца)

определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.

Свойства определителей.

1°. Определитель не изменится, если строки определителя заменить столб-

цами, а столбцы-соответствующими строками.

2°. Общий множитель элементов какой-нибудь строки (или столбца) может

быть вынесен за знак определителя.

3°. Если элементы одной строки (столбца) определителя соответственно

равны элементам другой строки (столбца), то определитель равен нулю.

4°. При перестановке двух строк (столбцов) определитель меняет знак на

противоположный.

5°. Определитель не изменится, если к элементам одной строки (столбца)

прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число (теорема о линейной комбинации параллельных рядов определителя).

Решение системы трех линейных уравнений с тремя неизвестными .

находится по формулам Крамера

При этом предполагается, что D ≠0 (если D = 0, то исходная система либо неопределенная, либо несовместная).

Если,система однородная, т. е. имеет вид

и ее определитель отличен от нуля, то она имеет единственное решение х= 0,

Если же определитель однородной системы равен нулю, то система сводится

либо к двум независимым уравнениям (третье является их следствием), либо к

одному уравнению (остальные два являются его следствиями). Первый случай

имеет место тогда, когда среди миноров определителя однородной системы есть

хотя бы один отличный от нуля, второй-тогда, когда все миноры этого опреде лителя равны нулю. В обоих случаях однородная система имеет бесчисленное множество решений.

Вычислить определитель третьего порядка

Габриель Крамер – математик, создатель одноименного метода решения систем линейных уравнений

Габриель Крамер – известный математик, который родился 31 июля 1704 года. Ещё в детстве Габриель поражал своими интеллектуальными способностями, особенно в области математики. Когда Крамеру было 20 лет, он устроился в Женевский университет штатным преподавателем.

Во время путешествия по Европе Габриель познакомился с математиком Иоганном Бернулли, который и стал его наставником. Только благодаря Иоганну, Крамер написал много статей по геометрии, истории математики и философии. А в свободное от работы время изучал математику всё больше и больше.

Наконец-то наступил тот день, когда Крамер нашёл способ, при помощи которого можно было бы легко решать не только лёгкие, но и сложные системы линейных уравнений.

В 1740 году у Крамера были опубликованы несколько работ, где доступно изложено решение квадратных матриц и описан алгоритм, как находить обратную матрицу . Далее математик описывал нахождения линейных уравнений разной сложности, где можно применить его формулы. Поэтому тему так и назвали: «Решение систем линейных уравнений методом Крамера».

Учёный умер в возрасте 48 лет (в 1752 году). У него было ещё много планов, но, к сожалению, он так и не успел их осуществить.

Пусть дана система линейных уравнений такого вида:

где , , – неизвестные переменные, – это числовые коэффициенты, в – свободные члены.

Решением СЛАУ (систем линейных алгебраических уравнение) называются такие неизвестные значения при которых все уравнения данной системы преобразовываются в тождества.

Если записать систему в матричном виде, тогда получается , где

В данной главной матрице находятся элементы, коэффициенты которых при неизвестных переменных,

Это матрица-столбец свободных членов, но есть ещё матрица-столбец неизвестных переменных:

После того, когда найдутся неизвестные переменные, матрица и будет решением системы уравнений, а наше равенство преобразовывается в тождество. . Если умножить , тогда . Получается: .

Если матрица – невырожденная, то есть, её определитель не равняется нулю, тогда у СЛАУ есть только одно единственное решение, которое находится при помощи метода Крамера.

Как правило, для решения систем линейных уравнений методом Крамера, нужно обращать внимания на два свойства, на которых и основан данный метод:

1. Определитель квадратной матрицы равняется сумме произведений элементов любой из строк (столбца) на их алгебраические дополнения:

Здесь – 1, 2, …, n; – 1, 2, 3, …, n.

2. Сумма произведений элементов данной матрицы любой строки или любого столбца на алгебраические дополнения определённых элементов второй строки (столбца) равняется нулю:

где – 1, 2, …, n; – 1, 2, 3, …, n. .

Итак, теперь можно найти первое неизвестное . Для этого необходимо умножить обе части первого уравнения системы на , части со второго уравнения на , обе части третьего уравнения на и т. д. То есть, каждое уравнение одной системы нужно умножать на определённые алгебраические дополнения первого столбца матрицы :

Теперь прибавим все левые части уравнения, сгруппируем слагаемые, учитывая неизвестные переменные и приравняем эту же сумму к сумме правых частей системы уравнения:

Можно обратиться к вышеописанным свойствам определителей и тогда получим:

И предыдущее равенство уже выглядит так:

Откуда и получается .

Аналогично находим . Для этого надо умножить обе части уравнений на алгебраические дополнения, которые находятся во втором столбце матрицы .

Теперь нужно сложить все уравнения системы и сгруппировать слагаемые при неизвестных переменных. Для этого вспомним свойства определителя:

Откуда получается .

Аналогично находятся все остальные неизвестные переменные.

Если обозначить:

тогда получаются формулы, благодаря которым находятся неизвестные переменные методом Крамера:

Замечание.

Тривиальное решение при может быть только в том случае, если система уравнений является однородной . И действительно, если все свободные члены нулевые, тогда и определители равняются нулю, так как в них содержится столбец с нулевыми элементами. Конечно же, тогда формулы , , дадут

Метод Крамера – теоремы

Прежде чем решать уравнение, необходимо знать:

1. теорему аннулирования;
2. теорему замещения.

Теорема замещения

Теорема

Сумма произведений алгебраических дополнений любого столбца (строки) на произвольные числа равняется новому определителю, в котором этими числами заменены соответствующие элементы изначального определителя, что отвечают данным алгебраическим дополнениям.

Например,

где – алгебраические дополнения элементов первого столбца изначального определителя:

Теорема аннулирования

Теорема

Сумма произведений элементов одной строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равняется нулю.

Например:

Алгоритм решения уравнений методом Крамера

Метод Крамера – простой способ решения систем линейных алгебраических уравнений. Такой вариант применяется исключительно к СЛАУ, у которых совпадает количество уравнений с количеством неизвестных, а определитель отличен от нуля.

Итак, когда выучили все этапы, можно переходить к самому алгоритму решения уравнений методом Крамера. Запишем его последовательно:

Шаг 1. Вычисляем главный определитель матрицы

и необходимо убедиться, что определитель отличен от нуля (не равен нулю).

Шаг 2. Находим определители

Это и есть определители матриц, которые получались из матрицы при замене столбцов на свободные члены.

Шаг 3. Вычисляем неизвестные переменные

Теперь вспоминаем формулы Крамера, по которым вычисляем корни (неизвестные переменные):

Шаг 4. Выполняем проверку

Выполняем проверку решения при помощи подстановки в исходную СЛАУ. Абсолютно все уравнения в системе должны быть превращены в тождества. Также можно высчитать произведение матриц . Если в итоге получилась матрица, которая равняется , тогда система решена правильно. Если же не равняется , скорей всего в одном из уравнений есть ошибка.

Давайте для начала рассмотрим систему двух линейных уравнений, так как она более простая и поможет понять, как правильно использовать правило Крамера. Если вы поймёте простые и короткие уравнения, тогда сможете решить более сложные системы трёх уравнений с тремя неизвестными.

Кроме всего прочего, есть системы уравнений с двумя переменными, которые решаются исключительно благодаря правилу Крамеру.

Итак, дана система двух линейных уравнений:

Для начала вычисляем главный определитель (определитель системы):

Значит, если , тогда у системы или много решений, или система не имеет решений. В этом случае пользоваться правилом Крамера нет смысла, так как решения не получится и нужно вспоминать метод Гаусса , при помощи которого данный пример решается быстро и легко.

В случае, если , тогда у система есть всего одно решение, но для этого необходимо вычислить ещё два определителя и найти корни системы.

Часто на практике определители могут обозначаться не только , но и латинской буквой , что тоже будет правильно.

Корни уравнения найти просто, так как главное, знать формулы:

Так как мы смогли решить систему двух линейных уравнений, теперь без проблем решим и систему трёх линейных уравнений, а для этого рассмотрим систему:

Здесь алгебраические дополнения элементов – первый столбец . Во время решения не забывайте о дополнительных элементах. Итак, в системе линейных уравнений нужно найти три неизвестных – при известных других элементах.

Создадим определитель системы из коэффициентов при неизвестных:

Умножим почленно каждое уравнение соответственно на , , – алгебраические дополнения элементов первого столбца (коэффициентов при ) и прибавим все три уравнения. Получаем:

Согласно теореме про раскладывание, коэффициент при равняется . Коэффициенты при и будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается

После этого можно записать равенство:

Для нахождения и перемножим каждое из уравнений изначальной системы в первом случае соответственно на , во втором – на и прибавим. Впоследствии преобразований получаем:

Если , тогда в результате получаем формулы Крамера:

Порядок решения однородной системы уравнений

Отдельный случай – это однородные системы:

Среди решений однородной системы могут быть, как нулевые решения , так и решения отличны от нуля.

Теорема

Если определитель однородной системы (3) отличен от нуля , тогда у такой системы может быть только одно решение.

Действительно, вспомогательные определители , как такие у которых есть нулевой столбец и поэтому, за формулами Крамера

Теорема

Если у однородной системы есть отличное от нуля решение, тогда её определитель равняется нулю

Действительно, пусть одно из неизвестных, например, , отличное от нуля. Согласно с однородностью Равенство (2) запишется: . Откуда выплывает, что

Примеры решения методом Крамера

Рассмотрим на примере решение методом Крамера и вы увидите, что сложного ничего нет, но будьте предельно внимательно, так как частые ошибки в знаках приводят к неверному ответу.

Пример 1

Задача

Решение

Первое, что надо сделать – вычислить определитель матрицы:

Как видим, , поэтому по теореме Крамера система имеет единственное решение (система совместна). Далее нужно вычислять вспомогательные определители. Для этого заменяем первый столбец из определителя на столбец свободных коэффициентов. Получается:

Аналогично находим остальные определители:

И проверяем:

Ответ

Пример 2

Задача

Решить систему уравнений методом Крамера:

Решение

Находим определители:

Ответ

= = = = = =

Проверка

Уравнение имеет единственное решение.

Ответ

Пример 3

Задача

Решить систему методом Крамера

Решение

Как вы понимаете, сначала находим главный определитель:

Как мы видим, главный определитель не равняется нулю и поэтому система имеет единственное решение. Теперь можно вычислить остальные определители:

При помощи формул Крамера находим корни уравнения:

Чтобы убедиться в правильности решения, необходимо сделать проверку:

Как видим, подставив в уравнение решённые корни, у нас ответ получился тот же, что и в начале задачи, что говорит о правильном решении уравнений.

Ответ

Система уравнений имеет единственное решение: , , .

Есть примеры, когда уравнение решений не имеет. Это может быть в том случае, когда определитель системы равен нулю, а определители при неизвестных неравны нулю. В таком случае говорят, что система несовместна, то есть не имеет решений. Посмотрим на следующем примере, как такое может быть.

Пример 4

Задача

Решить систему линейных уравнений методом Крамера:

Решение

Как и в предыдущих примерах находим главный определитель системы:

В этой системе определитель равняется нулю, соответственно, система несовместна и определенна или же несовместна и не имеет решений. Чтобы уточнить, надо найти определители при неизвестных так, как мы делали ранее:

Мы нашли определители при неизвестных и увидели, что все они не равны нулю. Поэтому система несовместна и не имеет решений.

Ответ

Система не имеет решений.

Часто в задачах на системы линейных уравнений встречаются такие уравнения, где есть не одинаковые буквы, то есть, кроме букв, которые обозначают переменные, есть ещё и другие буквы и они обозначают некоторое действительное число. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. Давайте и рассмотрим такой пример.

Используя формулы Крамера, находим:

Ответ

И наконец, мы перешли к самой сложной системе уравнений с четырьмя неизвестными. Принцип решения такой же, как и в предыдущих примерах, но в связи с большой системой можно запутаться. Поэтому рассмотрим такое уравнение на примере.

В изначальном определители из элементов второй строки мы отнимали элементы четвёртой строки, а из элементов третьей строки отнимались элементы четвёртой строки, которые умножались на 2. Также отнимали из элементов четвёртой строки элементы первой строки, умноженной на два. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Теперь можно находить определители при неизвестных:

Для преобразований определителя при четвёртом неизвестном из элементов первой строки мы вычитали элементы четвёртой строки.

Теперь по формулам Крамера нужно найти:

Ответ

Итак, мы нашли корни системы линейного уравнения:

Подведём итоги

При помощи метода Крамера можно решать системы линейных алгебраических уравнений в том случае, если определитель не равен нулю. Такой метод позволяет находить определители матриц такого порядка, как на благодаря формулам Крамера, когда нужно найти неизвестные переменные. Если все свободные члены нулевые, тогда их определители равны нулю, так как в них содержится столбец с нулевыми элементами. И конечно же, если определители равняются нулю, лучше решать систему методом Гаусса Метод Крамера в Excel от 2007 (XLSX)

Метод Крамера – теорема, примеры решений обновлено: 22 ноября, 2019 автором: Научные Статьи.Ру

Курсовая: Определители и системы линейных уравнений

1. Определители второго и третьего порядков и их свойства

1.1. Понятие матрицы и определителя второго порядка

Прямоугольную таблицу из чисел,

матрицей. Для обозначения матрицы используют либо сдвоенные вертикальные

черточки, либо круглые скобки. Например:

1 7 9.2 1 7 9.2

28 20 18 28 20 18

6 11 2 -6 11 2

Если число строк матрицы совпадает с числом ее столбцов, то матрица называется

квадратной. Числа, входящие в состав матрицы, называют ее элементами .

Рассмотрим квадратную матрицу, состоящую из четырех элементов:

Определителем второго порядка, соответствующим матрице (3.1), называется число,

и обозначаемое символом

Итак, по определению

Элементы, составляющие матрицу данного определителя, обычно называют

элементами этого определителя.

Справедливо следующее утверждение: для того чтобы определитель второго

порядка был равен нулю, необходимо и достаточно, чтобы элементы его строк (или

соответственно его столбцов) были пропорциональны .

Для доказательства этого утверждения достаточно заметить, что каждая из

пропорций /

эквивалентна равенству

А последнее равенство в силу (3.2) эквивалентно обращению в нуль определителя.

1.2. Система двух линейных уравнений с двумя неизвестными

Покажем, как применяются определители второго порядка для исследования и

отыскания решений системы двух линейных уравнений с двумя неизвестными

(коэффициенты ,

и свободные члены ,

считаются при этом заданными). Напомним, что пара чисел

Называется

решением системы (3.3), если подстановка этих чисел на место

и в данную систему

обращает оба уравнения (3.3) в тождества.

Умножая первое уравнение системы (3.3) на -

А второе - на -и

затем складывая полученные при этом равенства, получим

Аналогично путем умножения уравнений (3.3) на -исоответственно получим:

Введем следующие обозначения:

С помощью этих обозначений и выражения для определителя второго порядка

уравнения (3.4) и (3.5) могут быть переписаны в виде:

Определитель ,

составленный из коэффициентов при неизвестных системы (3.3), принято называть

определителем этой системы . Заметим, что определители

и получаются из

определителя системы

посредством замены его первого или соответственно второго столбца свободными

Могут представиться два случая: 1) определитель системы

отличен от нуля; 2) этот определитель равен нулю.

Рассмотрим сначала случай

0. Из уравнений (3.7) мы сразу же получаем формулы для неизвестных,

называемые формулами Крамера :

Полученные формулы Крамера (3.8) дают решение системы (3.7) и потому доказывают

единственность решения исходной системы (3.3). В самом деле, система (3.7)

является следствием системы (3.3), поэтому всякое решение системы (3.3) (в

случае, если оно существует!) должно являться решением и системы (3.7). Итак,

пока доказано, что если у исходной системы (3.3) существует при

0 решение, то это решение однозначно определяется формулами Крамера (3.8).

Легко убедиться и в существовании решения, т. е. в том. что при

0 два числа и

Определяемые формулами Крамера (3.8). будучи поставлены на место неизвестных в

уравнения (3.3), обращают эти уравнения в тождества. (Предоставляем читателю

самому расписать выражения для определителей

И убедиться в справедливости указанных тождеств.)

Мы приходим к следующему выводу: если определитель

системы (3.3) отличен от нуля, то существует, и притом единственное решение этой

системы, определяемое формулами Крамера (3.8).

Рассмотрим теперь случай, когда определитель

системы равен нулю . Могут представиться два подслучая : а) хотя

бы один из определителей

или , отличен от

нуля; б) оба определителя

и равны нулю. (если

определитель и

один из двух определителей

и равны нулю, то и

другой из указанных двух определителей равен нулю. В самом деле, пусть,

например = 0

Тогда из этих пропорций получим, что

В подслучае а) оказывается невозможным хотя бы одно из равенств (3.7), т. е.

система (3.7) не имеет решений, а поэтому не имеет решений и исходная система

(3.3) (следствием которой является система (3.7)).

В подслучае б) исходная система (3.3) имеет бесчисленное множество решений. В

самом деле, из равенств

0 и из утверждения в конце разд. 1.1 заключаем, что второе уравнение системы

(3.3) является следствием первого и его можно отбросить. Но одно уравнение с

двумя неизвестными

имеет бесконечно много решений (хотя бы один из коэффициентов

Или отличен от

нуля, и стоящее при нем неизвестное может быть определено из уравнения (3.9)

через произвольно заданное значение другого неизвестного).

Таким образом, если определитель

системы (3.3) равен нулю, то система (3.3) либо вовсе не имеет решений (в

случае, если хотя бы один из определителей

или отличен от

нуля), либо имеет бесчисленное множество решений (в случае, когда

0). В последнем

случае два уравнения (3.3) можно заменить одним и при решении его одно

неизвестное задавать произвольно.

Замечание . В случае, когда свободные члены

и равны нулю,

линейная система (3.3) называется однородной . Отметим, что однородная

система всегда имеет так называемое тривиальное решение:

0, = 0 (эти два

числа обращают оба однородных уравнения в тождества).

Если определитель однородной системы

отличен от нуля, то эта система имеет только тривиальное решение. Если же

= 0, то однородная система имеет бесчисленное множество решений (поскольку

для однородной системы возможность отсутствия решений исключена). Таким

образом, однородная система имеет нетривиальное решение в том и только в

том случае, когда определитель ее равен нулю.